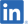Dr Maiti will present a seminar on "Entanglement and Majorana edge modes in the Kitaev model" on 13th December at 10:30 in L112. Everybody is welcome!
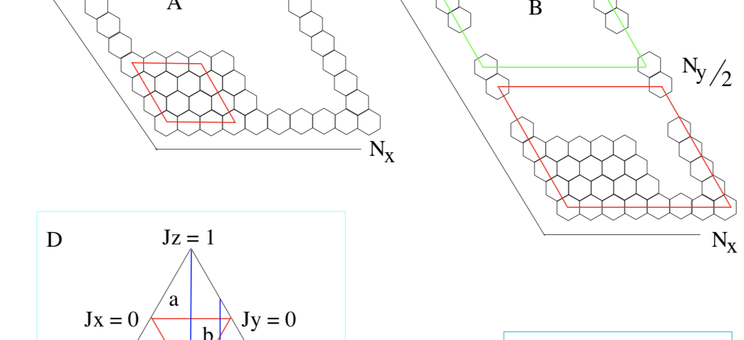
Abstract: We investigate entanglement measures in an exactly solvable 2D quantum spin model, namely, the Kitaev model. The Kitaev model on the honeycomb lattice is an example of a system with long-range entanglement (LRE) having intrinsic topological order and are known to exhibit exotic properties as topologically dependent degenerate ground states, fractional excitations and so on. I will discuss analysis of the von Neumann entanglement entropy and Schmidt gap in the vortex-free ground state of the Kitaev model for square/rectangular and cylindrical subsystems and
show how the gapless edge states influence the qualitative behaviour of these measures.